深入理解 python 虚拟机:多继承与 mro
在本篇文章当中将主要给大家介绍 python 当中的多继承和 mro,通过介绍在多继承当中存在的问题就能够理解在 cpython 当中引入 c3 算法的原因了,从而能够帮助大家更好的了理解 mro 。
python 继承的问题
继承是一种面向对象编程的概念,它可以让一个类(子类)继承另一个类(父类)的属性和方法。子类可以重写父类的方法,或者添加自己的方法和属性。这种机制使得代码可以更加模块化和易于维护。在 Python 中,继承是通过在子类的定义中指定父类来实现的。例如:
class Animal:
def __init__(self, name):
self.name = name
def speak(self):
raise NotImplementedError("Subclass must implement abstract method")
class Dog(Animal):
def speak(self):
return "woof"在这个例子中,我们定义了一个 Animal 类和一个 Dog 类。Dog 类继承了 Animal 类,并且重写了 speak 方法。此时,如果我们创建一个 Dog 实例并调用 speak 方法,它将返回 "woof"。
父类的修改会影响子类
当你修改父类的代码时,可能会影响到继承自它的子类。这是因为子类继承了父类的所有属性和方法,包括它们的实现。如果你修改了父类的实现,可能会导致子类的行为发生变化。因此,在修改父类代码时,你需要仔细考虑这个问题,并尽量避免对子类的影响。
多层继承的复杂性
在面向对象编程中,有时需要多层继承,即一个类继承自另一个继承自另一个类。这会导致代码的复杂性增加,因为你需要考虑每个类之间的关系和可能出现的命名冲突。另外,多层继承也会增加代码的耦合性,使得代码难以重构和维护。
多继承当中一个非常经典的问题就是棱形继承,菱形继承是指一个子类继承了两个父类,而这两个父类又继承自同一个基类的情况,如下图所示:
A
/ \
B C
\ /
D在这种情况下,子类 D 会继承两份来自基类 A 的属性和方法,这可能会导致一些不必要的问题。例如,如果基类 A 中有一个名为 foo() 的方法,而基类 B 和 C 都分别重写了这个方法,并在子类 D 中调用了这个方法,那么子类 D 就无法确定应该调用哪个版本的 foo() 方法。
另外一种情况就是在多继承的时候不同的基类定义了同样的方法,那么子类就无法确定应该使用哪个父类的实现。例如,考虑下面这个示例:
class A:
def method(self):
print('A')
class B:
def method(self):
print('B')
class C(A, B):
pass
c = C()
c.method() # 输出什么?在这个示例中,类 C 继承了类 A 和类 B 的 method 方法,但是这两个方法具有相同的方法名和参数列表。因此,当我们调用 c.method() 方法时,Python 将无法确定应该使用哪个父类的实现。
为了解决上面所提到的问题,Python 提供了方法解析顺序(Method Resolution Order,MRO)算法,这个算法可以帮助 Python 确定方法的调用顺序,也就是在调用的时候确定调用哪个基类的方法。
MRO
在 Python 中,多重继承会引起 MRO(Method Resolution Order,方法解析顺序)问题。当一个类继承自多个父类时,Python 需要确定方法调用的顺序,即优先调用哪个父类的方法。为了解决这个问题,Python 实现了一种称为 C3算法的 MRO 算法,它是一种确定方法解析顺序的算法。
我们先来体验使用一下 python 的 mro 的结果是什么样的,下面是一个使用多重继承的示例:
class A:
pass
class B(A):
pass
class C(A):
pass
class D(B, C):
pass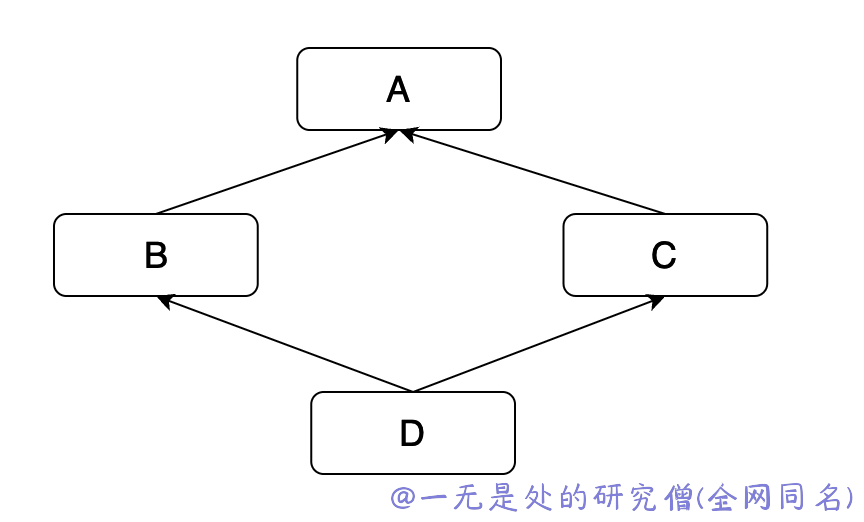
在这个示例中,D 类继承自 B 类和 C 类,而 B 和 C 又都继承自 A 类。因此,D 类的 MRO 列表如下所示:
[D, B, C, A]这个列表的解析顺序为 D -> B -> C -> A,也就是说,当我们调用 D 类的方法时,Python 会首先查找 D 类的方法,然后查找 B 类的方法,再查找 C 类的方法,最后查找 A 类的方法。
你可能会有疑问,为什么 cpython 需要这样去进行解析,为什么不在解析完类 B 之后直接解析 A,还要解析完类 C 之后再去解析 A,我们来看下面的代码:
class A:
def method_a(self):
print("In class A")
class B(A):
pass
class C(A):
def method_a(self):
print("In class C")
class D(B, C):
pass
if __name__ == '__main__':
obj = D()
print(D.mro())
obj.method_a()上面的代码输出结果如下所示:
[<class '__main__.D'>, <class '__main__.C'>, <class '__main__.B'>, <class '__main__.A'>, <class 'object'>]
In class C在上面的代码当中继承体系也是棱形继承,在类 A 当中有一个方法 method_a 其中类 B 继承了 A 但是没有重写这个方法,类 B 继承自 A 但是重写了这个方法,类 D 同时继承了类 B 和类 C,当对象 obj 调用方法 method_a 的时候发现在类 B 当中没有这个方法,这个时候如果直接在类 A 查找这个方法在很多情况下并不是我们想要的,因为 D 继承了 C 如果 C 重写了这个方法的话我们应该需要调用类 C 的 method_a 方法,而不是调用类 A 的 method_a 。
从上面的案例我们可以知道,一个子类不能够跨过他的直接父类(D 的直接父类就是 B 和 C)调用更上层的方法,而是先需要在所有的直接父类查看是否有这个方法,在 cpython 的 mro 实现当中是能够保证这一点的,这种性质叫做“单调性”(monotonicity)。
C3 算法
C3 算法是 Python 中使用的 MRO 算法,它可以用来确定一个类的方法解析顺序。首先我们需要知道的就是,当一个类所继承的多个类当中有相同的基类或者定义了名字相同的方法,会是一个问题。mro 就是我给他一个对象,他会给我们返回一个类的序列,当我们打算从对象当中获取一个属性或者方法的时候就会顺着这个序列从左往右进行查找,若查找成功则返回,否则继续查找后续的类。
现在我们来详细介绍一下 C3 算法的实现细节,这个算法的主要流程是一个递归求解 mro 的过程,假设 A 继承自 [B, C, D, E, F],那么 C3 算法求 mro 的实现流程如下所示:
- mro(A) = [A] + merge(mro(B), mro(C), mro(D), mro(E), mro(F), [B, C, D, E, F] )
- merge 函数的原理是遍历传入的序列,找到一个这样的序列,序列的第一个类型只能在其他序列的头部,或者没有在其他序列出现,并且将这个序列加入到 merge 函数的返回序列当中,并且将这个类从所有序列当中删除,重复这个步骤直到所有的序列都为空。
class O
class A extends O
class B extends O
class C extends O
class D extends O
class E extends O
class K1 extends A, B, C
class K2 extends D, B, E对 K2 求 mro 序列的结果如下所示:
L(K2) := [K2] + merge(L(D), L(B), L(E), [D, B, E])
= [K2] + merge([D, O], [B, O], [E, O], [D, B, E]) // 选择D
= [K2, D] + merge([O], [B, O], [E, O], [B, E]) // 不选O,选择B 因为 O 在 [B, O] 和 [E, O] 当中出现了而且不是第一个
= [K2, D, B] + merge([O], [O], [E, O], [E]) // 不选O,选择E 因为 O 在 [E, O] 当中出现了而且不是第一个
= [K2, D, B, E] + merge([O], [O], [O]) // 选择O
= [K2, D, B, E, O]我们自己实现的 mro 算法如下所示:
from typing import Iterable
class A:
pass
class B(A):
pass
class C(A):
pass
class D(B, C):
pass
def mro(_type: type):
bases = _type.__bases__
lin_bases = []
for base in bases:
lin_bases.append(mro(base))
lin_bases.append(list(bases))
return [_type] + merge(lin_bases)
def merge(types: Iterable[Iterable[type]]):
res = []
seqs = types
while True:
seqs = [s for s in seqs if s]
if not seqs:
# if seqs is empty
return res
for seq in seqs:
head = seq[0]
if not [s for s in seqs if head in s[1:]]:
break
else:
# 如果遍历完所有的类还是找不到一个合法的类 则说明 mro 算法失败 这个继承关系不满足 C3 算法的要求
raise Exception('can not find mro sequence')
res.append(head)
for s in seqs:
if s[0] == head:
del s[0]
if __name__ == '__main__':
print(D.mro())
print(mro(D))
assert D.mro() == mro(D)上面的程序的输出结果如下所示:
[<class '__main__.D'>, <class '__main__.B'>, <class '__main__.C'>, <class '__main__.A'>, <class 'object'>]
[<class '__main__.D'>, <class '__main__.B'>, <class '__main__.C'>, <class '__main__.A'>, <class 'object'>]只需要理解求解 mro 序列的过程,上面的代码比较容易理解,首先就是递归求解各个父类的 mro 序列,然后将他们按照从左到右的顺序放入到一个列表当中,最终将父类的 mro 序列进行 merge 操作,返回结果即可。
merge 函数的主要操作为,按照从左到右的顺序遍历各个父类的 mro 序列,如果第一个类没有在其他父类的 mro 序列当中出现,或者是其他父类 mro 序列当中的第一个类的话就可以将这个类加入到返回的 mro 列表当中,否则选择下一个类的 mro 序列进行相同的操作,直到找到一个符合上面条件的类,如果遍历完所有的父类还是没有找到的话那么就报错。
Mypy 针对 mro 实现
mypy 是一个 python 类型的静态分析工具,它也实现了 C3 算法用于计算 mro ,下面是它的代码实现。
class MroError(Exception):
"""Raised if a consistent mro cannot be determined for a class."""
def linearize_hierarchy(
info: TypeInfo, obj_type: Callable[[], Instance] | None = None
) -> list[TypeInfo]:
# TODO describe
if info.mro:
return info.mro
bases = info.direct_base_classes()
if not bases and info.fullname != "builtins.object" and obj_type is not None:
# Probably an error, add a dummy `object` base class,
# otherwise MRO calculation may spuriously fail.
bases = [obj_type().type]
lin_bases = []
for base in bases:
assert base is not None, f"Cannot linearize bases for {info.fullname} {bases}"
lin_bases.append(linearize_hierarchy(base, obj_type))
lin_bases.append(bases)
return [info] + merge(lin_bases)
def merge(seqs: list[list[TypeInfo]]) -> list[TypeInfo]:
seqs = [s.copy() for s in seqs]
result: list[TypeInfo] = []
while True:
seqs = [s for s in seqs if s]
if not seqs:
return result
for seq in seqs:
head = seq[0]
if not [s for s in seqs if head in s[1:]]:
break
else:
raise MroError()
result.append(head)
for s in seqs:
if s[0] is head:
del s[0]上面的函数 linearize_hierarchy 就是用于求解 mro 的函数,上面的实现整体过程和我们自己实现的 C3 算法是一样的,首先递归调用 linearize_hierarchy 计算得到父类的 mro 序列,最后将得到的 mro 进行 merge 操作。
cpython 虚拟机 mro 实现
在本小节当中主要给大家介绍一下在 cpython 当中 C 语言层面是如何实现 mro 的。需要知道的 cpython 对于 mro 的实现也是使用我们在上面提到的算法,算法原理也是一样的。
static PyObject *
mro_implementation(PyTypeObject *type)
{
PyObject *result;
PyObject *bases;
PyObject **to_merge;
Py_ssize_t i, n;
if (type->tp_dict == NULL) {
if (PyType_Ready(type) < 0)
return NULL;
}
// 获取类型 type 的所有父类
bases = type->tp_bases;
// bases 的数据类型为 tuple
assert(PyTuple_Check(bases));
n = PyTuple_GET_SIZE(bases);
// 检查基类的 mro 序列是否计算出来了
for (i = 0; i < n; i++) {
PyTypeObject *base = (PyTypeObject *)PyTuple_GET_ITEM(bases, i);
if (base->tp_mro == NULL) {
PyErr_Format(PyExc_TypeError,
"Cannot extend an incomplete type '%.100s'",
base->tp_name);
return NULL;
}
assert(PyTuple_Check(base->tp_mro));
}
// 如果是单继承 也就是只继承了一个类 那么就可以走 fast path
if (n == 1) {
/* Fast path: if there is a single base, constructing the MRO
* is trivial.
*/
PyTypeObject *base = (PyTypeObject *)PyTuple_GET_ITEM(bases, 0);
Py_ssize_t k = PyTuple_GET_SIZE(base->tp_mro);
result = PyTuple_New(k + 1);
if (result == NULL) {
return NULL;
}
// 直接将父类的 mro 序列加在 当前类的后面 即 mro = [当前类, 父类的 mro 序列]
Py_INCREF(type);
PyTuple_SET_ITEM(result, 0, (PyObject *) type);
for (i = 0; i < k; i++) {
PyObject *cls = PyTuple_GET_ITEM(base->tp_mro, i);
Py_INCREF(cls);
PyTuple_SET_ITEM(result, i + 1, cls);
}
return result;
}
/* This is just a basic sanity check. */
if (check_duplicates(bases) < 0) {
return NULL;
}
/* Find a superclass linearization that honors the constraints
of the explicit tuples of bases and the constraints implied by
each base class.
to_merge is an array of tuples, where each tuple is a superclass
linearization implied by a base class. The last element of
to_merge is the declared tuple of bases.
*/
// 如果是多继承就要按照 C3 算法进行实现了
to_merge = PyMem_New(PyObject *, n + 1);
if (to_merge == NULL) {
PyErr_NoMemory();
return NULL;
}
// 得到所有父类的 mro 序列,并将其保存到 to_merge 数组当中
for (i = 0; i < n; i++) {
PyTypeObject *base = (PyTypeObject *)PyTuple_GET_ITEM(bases, i);
to_merge[i] = base->tp_mro;
}
// 和前面我们自己实现的算法一样 也要将所有基类放在数组的最后
to_merge[n] = bases;
result = PyList_New(1);
if (result == NULL) {
PyMem_Del(to_merge);
return NULL;
}
Py_INCREF(type);
PyList_SET_ITEM(result, 0, (PyObject *)type);
// 合并数组
if (pmerge(result, to_merge, n + 1) < 0) {
Py_CLEAR(result);
}
PyMem_Del(to_merge);
// 将得到的结果返回
return result;
}在上面函数当中我们可以分析出来整个代码的流程和我们在前面提到的 C3 算法一样,
static int
pmerge(PyObject *acc, PyObject **to_merge, Py_ssize_t to_merge_size)
{
int res = 0;
Py_ssize_t i, j, empty_cnt;
int *remain;
// remain[i] 表示 to_merge[i] 当中下一个可用的类 也就是说 0 - i-1 的类已经被处理合并了
/* remain stores an index into each sublist of to_merge.
remain[i] is the index of the next base in to_merge[i]
that is not included in acc.
*/
remain = PyMem_New(int, to_merge_size);
if (remain == NULL) {
PyErr_NoMemory();
return -1;
}
// 初始化的时候都是从第一个类开始的 所以下标初始化成 0
for (i = 0; i < to_merge_size; i++)
remain[i] = 0;
again:
empty_cnt = 0;
for (i = 0; i < to_merge_size; i++) {
PyObject *candidate;
PyObject *cur_tuple = to_merge[i];
if (remain[i] >= PyTuple_GET_SIZE(cur_tuple)) {
empty_cnt++;
continue;
}
/* Choose next candidate for MRO.
The input sequences alone can determine the choice.
If not, choose the class which appears in the MRO
of the earliest direct superclass of the new class.
*/
// 得到候选的类
candidate = PyTuple_GET_ITEM(cur_tuple, remain[i]);
// 查看各个基类的 mro 序列的尾部当中是否包含 candidate 尾部就是除去剩下的 mro 序列当中的第一个 剩下的类就是尾部当中含有的类 tail_contains 就是检查尾部当中是否包含 candidate
for (j = 0; j < to_merge_size; j++) {
PyObject *j_lst = to_merge[j];
if (tail_contains(j_lst, remain[j], candidate))
// 如果尾部当中包含 candidate 则说明当前的 candidate 不符合要求需要查看下一个 mro 序列的第一个类 看看是否符合要求 如果还不符合就需要找下一个 再进行重复操作
goto skip; /* continue outer loop */
}
// 找到了则将 candidate 加入的返回的结果当中
res = PyList_Append(acc, candidate);
if (res < 0)
goto out;
// 更新 remain 数组,在前面我们提到了当加入一个 candidate 到返回值当中的时候需要将这个类从所有的基类的 mro 序列当中删除 (事实上只可能删除各个 mro 序列当中的第一个类)因此需要更新 remain 数组
for (j = 0; j < to_merge_size; j++) {
PyObject *j_lst = to_merge[j];
if (remain[j] < PyTuple_GET_SIZE(j_lst) &&
PyTuple_GET_ITEM(j_lst, remain[j]) == candidate) {
remain[j]++;
}
}
goto again;
skip: ;
}
if (empty_cnt != to_merge_size) {
set_mro_error(to_merge, to_merge_size, remain);
res = -1;
}
out:
PyMem_Del(remain);
return res;
}
static int
tail_contains(PyObject *tuple, int whence, PyObject *o)
{
Py_ssize_t j, size;
size = PyTuple_GET_SIZE(tuple);
for (j = whence+1; j < size; j++) {
if (PyTuple_GET_ITEM(tuple, j) == o)
return 1;
}
return 0;
}再谈 MRO
在本篇文章当中主要给大家介绍了多继承存在的问题,以及介绍了在 python 当中的解决方案 C3 算法。之所以被称作 C3 算法,主要是因为这个算法有以下三点特性:
- a consistent extended precedence graph
- preservation of local precedence order
- fitting a monotonicity criterion
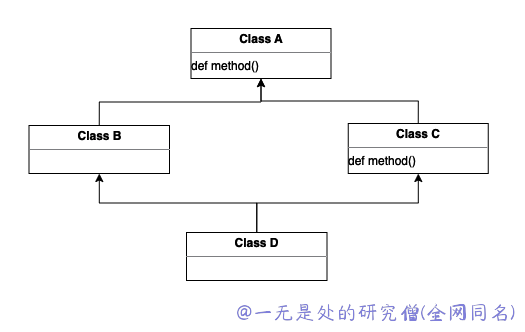
我们使用上面的图来分析一下上面的三个特性是在说明什么,在上面的继承关系当中类 A 当中有一个方法 method,类 B 和类 C 继承自类 A 并且类 C 重写了 method 方法,类 D 继承了 B 和 C 。
- monotonicity 单调性,这个特性主要是说明子类不能够跨过父类直接调用父类的父类的方法,比如在上面的类当中,当类 D 调用 method 方法的时候,调用的是类 C 的 method 方法而不是类 A 的 method 方法,虽然类 B 没有 method 而且类 A 有 method 方法,但是子类 D 不能够跨过父类 B 直接调用 类 A 的方法,必须检查类 C 是否有这个方法,如果有就调用 C 的,如果 B C 都没有才调用 A 的。
- preservation of local precedence order(保留局部优先顺序),这一点表示 mro 要保证按照继承先后的顺序去查找,也就是说先继承的先查找,比如 D(B, C) 那么如果同一个方法类 B 和类 C 都有,那么就会优先使用 B 当中的方法。
- a consistent extended precedence graph,这一点是相对来说比较复杂的,这个特性也是一个关于优先级的特性,是之前局部优先的扩展,他的意思是如果两个类 A B 有相同的方法,如果 A 或者 A 的子类出现在 B 或者 B 的子类之前,那么 A 的优先级比 B 高。比如说对于下图当中的继承关系 editable-scrollable-pane 继承自 scrollable-pane 和 editable-pane,editable-pane继承自 editing-mixin 和 pane,scrollable-pane 继承自 scrolling-mixin 和 pane。现在有一个 editable-scrollable-pane 对象调用一个方法,如果这个方法只在 scrolling-mixin 和 editing-mixin 当中出现,那么会调用 scrolling-mixin 当中的方法,不会调用 editing-mixin 当中的方法。这是因为对于 editable-scrollable-pane 对象来说 scrollable-pane 在 editable-pane 前面,而前者是 scrolling-mixin 的子类,后者是 editing-mixin 的子类,这是符合前面我们所谈到的规则。
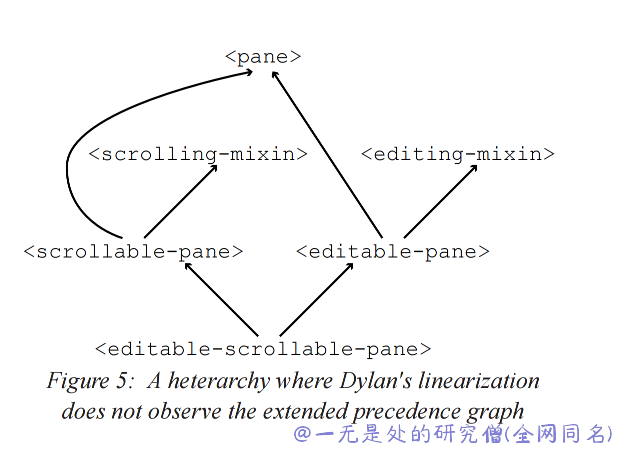
上图来自论文 A Monotonic Superclass Linearization for Dylan ,这篇论文便是 C3 算法的出处。如果你对这篇论文感兴趣的话,论文下载地址为 https://opendylan.org/_static/c3-linearization.pdf 。
总结
在本篇文章当中主要给大家详细分析了 python 当中是如何解决多继承存在的问题的,并且详细分析了 C3 算法以及他在 python 和虚拟机层面的实现,最后简要介绍了 C3 算法的三个特性,通过仔细分析这三个特性可以帮助我们深入理解整个继承树的调用链,当然在实际编程当中最好使用更简洁的继承方式,这也可以避免很多问题。
本篇文章是深入理解 python 虚拟机系列文章之一,文章地址:https://github.com/Chang-LeHung/dive-into-cpython
更多精彩内容合集可访问项目:https://github.com/Chang-LeHung/CSCore
关注公众号:一无是处的研究僧,了解更多计算机(Java、Python、计算机系统基础、算法与数据结构)知识。
